Catégorisation des exercices de musculation : analyse des clusters, visualisations et critique (Partie 3)

Cette troisième partie présente l’interprétation du clustering IA pour la catégorisation des exercices de musculation en visualisant les regroupements via t-SNE et dendrogramme.

Dans les deux premières parties, nous avons vu comment préparer les données et exécuter l’algorithme de clustering K‑Means pour déterminer une valeur de K pertinente. Ici, nous analysons les résultats obtenus, comparons différentes valeurs de K (25 vs 36) et utilisons des visualisations pour interpréter les clusters. Enfin, nous discutons des limites de la méthode et du dataset, et proposons des pistes d’amélioration.

Exécution du clustering K‑Means et analyse

Exécution du clustering avec K=36

L’analyse des scores (silhouette score et Calinski‑Harabasz) a montré que K=36 segmente finement l’espace des exercices. Nous exécutons ci‑dessous K‑Means avec K=36 pour illustrer la répartition des clusters et identifier les groupes cohérents vs les clusters trop spécifiques.

# ...

# Choix du nombre de clusters
k = 36

model = KMeans(n_clusters=k, random_state=0)

fdf = df.copy()
fdf["cluster"] = model.fit_predict(nds)

print(fdf["cluster"].sort_values().to_string())

Résultats du clustering

L’exécution du modèle permet d’assigner à chaque exercice un numéro de cluster. Les observations principales sont les suivantes :

• Plusieurs clusters sont cohérents et regroupent des exercices similaires (par exemple des exercices d’isolation ciblant le même muscle).
• Certains clusters sont très spécifiques et ne contiennent parfois qu’un seul exercice. C’est un cas fréquent pour des mouvements polyarticulaires du bas du corps où la sollicitation musculaire et la fatigue systémique varient.

Ces résultats illustrent le compromis classique en clustering : augmenter K améliore la granularité mais peut générer des clusters peu exploitables. Il faut croiser métriques (silhouette, Calinski-Harabasz) et validation métier pour choisir le meilleur K.

Exécution et analyse du clustering avec K=25

Les résultats obtenus avec K=36 sont intéressants mais manquent de pertinence. Pour affiner la catégorisation, nous pouvons réexécuter l’algorithme K-Means avec K=25 (le second pic de score de silhouette).

K=25 apparaît maintenant comme un bon compromis : les clusters sont plus denses et souvent plus exploitables pour une catégorisation pratique. Le principal inconvénient est la possible agrégation d’exercices qui ciblent le même muscle tout en ayant des profils biomécaniques différents (par exemple isolations vs polyarticulaires pour les pectoraux).

Visualisations : comment interpréter t-SNE et dendrogramme

Compte tenu de la quantité de données et du nombre de clusters, un expert métier pourrait évaluer qualitativement la pertinence des regroupements. Cependant, si vous n’avez pas cette expertise à disposition, il est possible de valider qualitativement les regroupements grâce à deux visualisations complémentaires :

• La réduction de dimension (t-SNE) : elle permet d’observer la séparation locale des clusters sur une carte 2D.
• Le dendrogramme : il met en évidence la hiérarchie des regroupements et les distances entre familles d’exercices.

Ces deux approches sont complémentaires et permettent d’apprécier visuellement la cohérence des clusters identifiés par l’algorithme K-Means.

Visualisation t-SNE des clusters

Le nombre de features de ce dataset est très élevé. Il est donc impossible de représenter ces données directement dans un espace 2D ou 3D. Pour contourner cette limitation, nous utilisons l’algorithme t-SNE qui permet de réduire la dimensionnalité tout en préservant les relations de proximité entre les points de données.

Dans notre cas, t-SNE peut réduire la matrice normalisée en deux composantes. Cela permet de visualiser les clusters dans un espace 2D où chaque exercice est représenté comme un point coloré.

Voici le code Python utilisé pour générer cette visualisation :

# ...

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=0, perplexity=10)
tsne_results = tsne.fit_transform(nds)

vis_df = pd.DataFrame({
    "x": tsne_results[:, 0],
    "y": tsne_results[:, 1],
    "cluster": fdf["cluster"],
    "exercise": fdf.index
})

plt.figure(figsize=(20, 12))
scatter = plt.scatter(
    vis_df["x"], vis_df["y"], c=vis_df["cluster"], cmap="viridis",
)
plt.colorbar(scatter)

for i, row in vis_df.iterrows():
    plt.annotate(row["exercise"], (row["x"], row["y"]), textcoords="offset points", xytext=(5, 5), fontsize=8)

plt.title("t-SNE Visualization of Exercises Clusters")
plt.xlabel("t-SNE Component 1")
plt.ylabel("t-SNE Component 2")
plt.tight_layout()
plt.show()

Après avoir exécuté ce script, nous obtenons une visualisation en 2D des exercices de musculation, où chaque point représente un exercice et la couleur indique le groupe auquel il appartient.

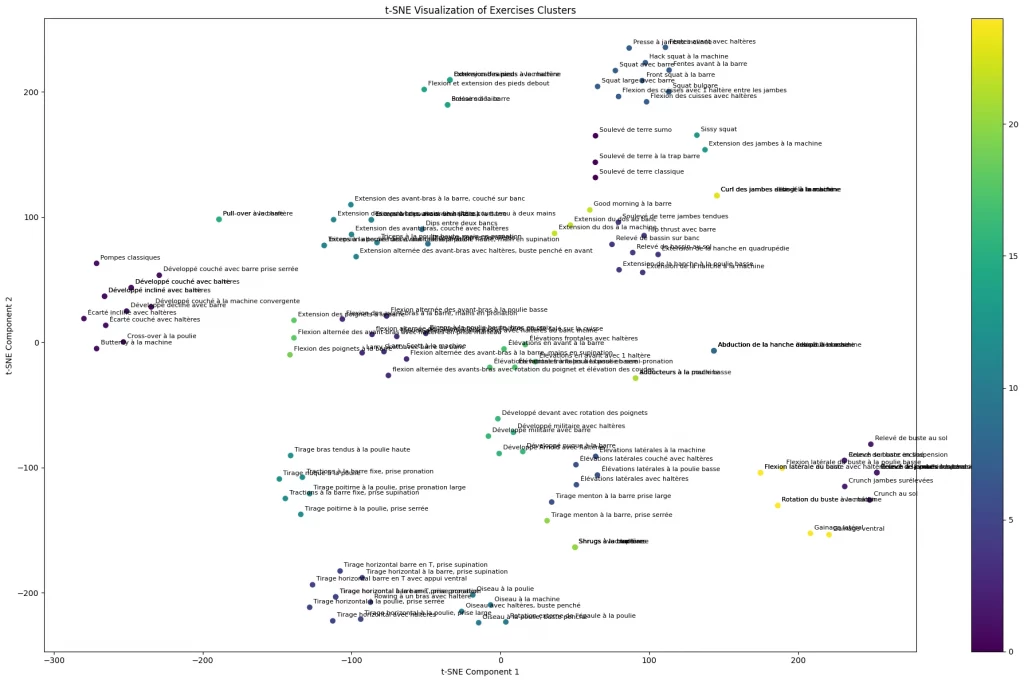
Globalement, on observe une bonne séparation des clusters, ce qui indique que l’algorithme K-Means a réussi à regrouper les exercices de manière cohérente en fonction de leurs caractéristiques.
De plus, on peut identifier visuellement le rapprochement entre certains clusters, ce qui peut refléter des similitudes dans les caractéristiques des exercices. On peut citer par exemple les exercices d’isolation des différentes portions du deltoïde qui sollicitent la même articulation et souvent les trapèzes supérieurs.

Dendrogramme : hiérarchie et interprétation

La seconde méthode de visualisation proposée est le dendrogramme. Un dendrogramme s’analyse généralement dans le cadre d’un clustering hiérarchique. Cette méthode de représentation semble pertinente compte tenu des muscles et parties du corps sollicités par les exercices de musculation.

Pour générer le dendrogramme, nous allons exécuter le code Python suivant :

# ...

from scipy.cluster.hierarchy import dendrogram, linkage

linked = linkage(nds, method="ward")

plt.figure(figsize=(12, 8))
dendrogram(
    linked,
    orientation="top",
    labels=fdf.index,
    distance_sort="descending",
    show_leaf_counts=True,
    color_threshold=linked[-(k-1), 2],
)
plt.title("Exercices Dendrogram")
plt.xlabel("Exercise Index")
plt.ylabel("Distance")
plt.show()

L’exécution de ce script permet de générer le dendrogramme suivant :

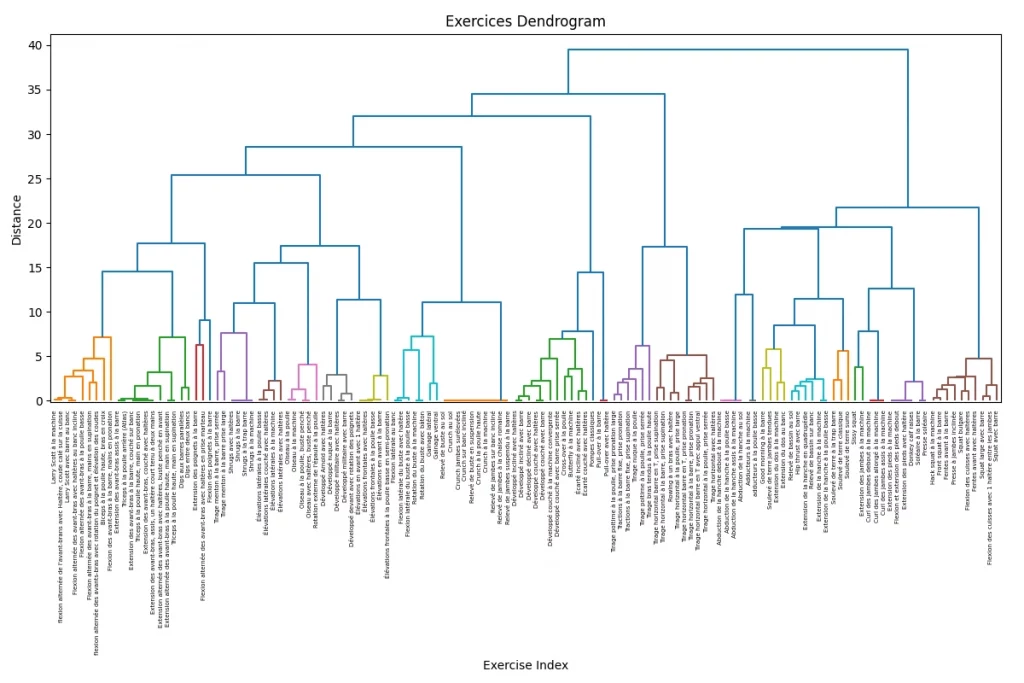
L’analyse du dendrogramme révèle que la majorité des regroupements se font à une distance maximale de 7 sur 40, ce qui témoigne d’une cohérence interne des clusters. Les groupes les plus homogènes correspondent souvent à des exercices d’isolation ciblant des muscles précis (grand droit, ischio-jambiers, adducteurs). À l’inverse, les clusters situés aux distances maximales réunissent des exercices plus variés (exercices polyarticulaires).

La structure hiérarchique du dendrogramme met également en évidence une séparation naturelle entre les exercices du haut et du bas du corps dès la première branche. Au sein de ces grandes familles, on observe des sous-catégories cohérentes : chaîne antérieure et postérieure du haut du corps, exercices d’isolation, etc. Cette organisation reflète la logique biomécanique sous-jacente à la classification.

Conclusion de l’analyse visuelle des catégories

En croisant ces deux visualisations (t-SNE et dendrogramme), on constate que les clusters générés par l’algorithme K-Means avec K=25 sont globalement pertinents et reflètent bien la diversité et la logique des exercices de musculation.

La combinaison de ces approches permet non seulement de valider la cohérence des regroupements, mais aussi d’identifier visuellement les proximités et les distinctions naturelles entre les différentes familles d’exercices. Cette méthodologie offre ainsi une base solide pour une catégorisation intelligente et exploitable des exercices de musculation.

Analyse critique de la méthode de catégorisation des exercices de musculation

Comparaison avec une classification humaine

Mon hypothèse initiale

Afin de valider la catégorisation d’exercices de musculation proposée par l’algorithme K-Means, j’ai élaboré une classification plus « humaine » basée sur mes connaissances en biomécanique, en anatomie fonctionnelle et sur mon expérience pratique :

• Haut du corps : j’ai distingué les exercices polyarticulaires des exercices d’isolation.
  • Les exercices polyarticulaires : j’ai séparé les exercices de poussée et de tirage, en tenant compte de l’axe du mouvement (horizontal ou vertical). Par exemple, les développés couchés et les pompes sont des exercices de poussée horizontale, tandis que les tractions sont des exercices de tirage vertical.
  • Les exercices d’isolation : ils sont regroupés selon le muscle principalement ciblé. Par exemple, les curls biceps ciblent le biceps brachial, les extensions triceps ciblent le triceps brachial, etc.
• Bas du corps : la catégorisation est plus complexe, notamment pour affiner les distinctions entre les différents exercices polyarticulaires comme le soulevé de terre, le squat ou les fentes avant. C’est précisément sur ce point que l’approche par clustering IA apporte une analyse complémentaire.

Ma catégorisation humaine a abouti à 24 catégories distinctes d’exercices.

Confrontation de l’hypothèse avec les résultats du clustering IA

Le clustering K-Means avec K=25 obtient un bon score de silhouette. Ce résultat, très proche de ma classification humaine à 24 catégories, montre une cohérence entre l’intuition métier et la classification automatique, tout en mettant en lumière des différences intéressantes sur certains mouvements hybrides.

Cependant, le modèle d’apprentissage non supervisé obtient des regroupements différents des miens. Par exemple, il a isolé certains exercices atypiques comme les pull-overs, qui sollicitent à la fois les pectoraux et le grand dorsal. Dans ma classification, j’ai fait abstraction de cette particularité pour privilégier la séparation du groupe des pectoraux afin de distinguer clairement les exercices polyarticulaires et d’isolations.
Ainsi, le clustering K-Means gomme certaines distinctions fines que j’aurais faites manuellement, en préférant mettre en lumière des proximités fonctionnelles parfois inattendues.

En résumé, la catégorisation automatique s’approche de l’hypothèse humaine sur le nombre de familles, mais propose des regroupements différents. Parfois elles sont plus pertinentes ou originales, notamment pour les exercices hybrides ou difficiles à classer. Mais, elle efface aussi certaines nuances importantes pour un programme de musculation ciblé.

Limites du dataset et pistes d’amélioration

Qualité du dataset

La pertinence des résultats d’une classification non supervisée dépend fortement de la qualité du dataset initial. La base de données utilisée ici présente plusieurs limites :

• Le nombre d’exercices (133) est relativement faible pour un algorithme de clustering. Pour l’algorithme K-Means, il est conseillé d’avoir un nombre d’échantillons bien plus élevé.
• La sélection des exercices peut conduire à une sur-représentation de certaines familles d’exercices, biaisant ainsi les clusters. Par exemple, il existe de nombreuses variantes de curls biceps, mais beaucoup moins d’exercices pour les deltoïdes postérieurs, les quadriceps ou les ischio-jambiers.
• La qualité des données dépend de l’analyse biomécanique initiale, qui est en partie subjective. Par exemple, l’évaluation de la fatigue systémique est difficile à quantifier précisément et peut varier selon les individus.
• La sélection des caractéristiques (features) influence fortement les résultats. Peut-être que d’autres caractéristiques auxquelles je n’ai pas pensé permettraient une meilleure catégorisation. De même, la pondération des caractéristiques, ou leur représentation numérique, peut biaiser les résultats.

Choix de l’algorithme

Le choix de l’algorithme K-Means, bien que pertinent pour cette tâche, présente certaines limites :

• K-Means regroupe les données en clusters sphériques (réduction de variance), ce qui peut effacer certains regroupements fins ou non linéaires dans les données.
• Les valeurs statistiquement aberrantes (outliers) peuvent fortement influencer les centres des clusters, conduisant à des regroupements moins pertinents. Les mouvements de pull-over en est probablement un bon exemple.
• K-Means nécessite de définir à l’avance le nombre de clusters (K), nous avons choisi K=25 basé sur les scores de silhouette et de Calinski-Harabasz, mais ce choix peut sembler arbitraire.

Perspectives d’amélioration

Pour améliorer la qualité et la pertinence des résultats, plusieurs axes d’amélioration sont possibles :

• Enrichir le dataset : ajouter davantage d’exercices, de variantes et de mouvements fonctionnels. Cela permettrait d’obtenir des clusters plus représentatifs et de limiter les biais de sélection.
• Affiner les caractéristiques : mieux définir et pondérer les features existantes, ou en intégrer de nouvelles comme l’amplitude du mouvement sur les articulations, l’étirement musculaire ou la courbe de résistance (forte tension d’étirement ou de contraction).
• Tester d’autres algorithmes : utiliser des méthodes de clustering alternatives (DBSCAN, modèles hiérarchiques, etc.) pour révéler des structures différentes ou complémentaires à celles de K-Means.

Conclusion

Le clustering K-Means appliqué aux 133 exercices montre que l’IA peut retrouver une structure proche de la catégorisation humaine tout en révélant des regroupements fonctionnels inattendus.

La démarche se décompose en plusieurs étapes clés pour aboutir à un modèle exploitable :

1. Prétraitement des données : nettoyer et normaliser les données pour garantir leur qualité et leur cohérence.
2. Sélection des caractéristiques : identifier et sélectionner les caractéristiques les plus pertinentes pour le clustering.
3. Choix de l’algorithme : sélectionner l’algorithme de clustering approprié (K-Means, DBSCAN, etc.) en fonction des données et des objectifs.
4. Évaluation des résultats : utiliser des métriques de validation (silhouette, Calinski-Harabasz) pour évaluer la qualité des clusters.
5. Itération : ajuster les paramètres, enrichir le dataset et tester d’autres algorithmes pour améliorer la pertinence des résultats.
6. Intégration : utiliser le modèle final pour catégoriser de nouveaux exercices ou suggérer des variantes d’exercices dans une application de coaching par exemple.

Vous avez des questions ? Vous adoptez une approche différente pour classifier vos données ? N’hésitez pas à laisser un commentaire pour enrichir la discussion.