Catégorisation IA des exercices de musculation : Feature extraction & Clustering K-Means (2/3)

Cet article explique, pas à pas, comment effectuer la feature extraction des exercices de musculation et appliquer un clustering K-Means pour les catégoriser.

Vous trouverez une méthodologie reproductible pour transformer vos données en vecteurs numériques, les normaliser et choisir le nombre optimal de clusters à l’aide de méthodes de scoring. L’objectif est d’obtenir une catégorisation d’exercices de musculation par IA fiable et interprétable, tout en optimisant les paramètres du K-Means pour éviter le sur-clustering.

Dataset d’exercices de musculation pour le clustering IA

Dans la première partie, nous avons vu comment définir et représenter les caractéristiques biomécaniques des exercices que nous voulons analyser. Le résultat final est un schéma JSON structuré qui présente les features de chaque exercice :

• Muscles sollicités (avec niveaux : principal, ciblé, secondaire, stabilisateur).
• Articulations impliquées.
• Plans de mouvement (sagittal, frontal, transverse).
• Fatigue systémique (indicateur relatif de fatigue systémique).

Stratégie IA pour catégoriser les exercices

Quelle est la meilleure approche pour catégoriser les exercices ?

Afin de choisir la meilleure approche, il est essentiel de prendre en compte :

• La nature des données disponibles : dans notre cas, nous disposons d’un dataset structuré avec des caractéristiques bien définies.
• L’objectif que nous souhaitons atteindre : regrouper les exercices similaires en catégories cohérentes inconnues à l’avance.

Quels modèles IA peuvent être utilisés ?

Pour atteindre cet objectif, nous pouvons envisager deux approches :

• Demander à un LLM de lire les caractéristiques des exercices et de les regrouper en catégories.
• Utiliser un modèle de machine learning classique pour regrouper les exercices similaires en catégories.

La première approche est simple et rapide à mettre en oeuvre. Nous n’avons qu’un seul prompt à écrire et nous déléguons le travail complet du dataset à l’IA. Cependant, cette approche risque de donner des résultats incohérents :

• Le LLM peut halluciner,
• La taille du contexte peut être insuffisante pour traiter l’ensemble du dataset,
• Les réponses peuvent être biaisées par les données sur lesquelles le modèle a été entraîné.

La seconde approche est plus complexe. Elle nécessite de choisir le bon modèle, de préparer les données en conséquence et de définir une méthodologie d’évaluation. Même si elle est plus longue à mettre en oeuvre, cette approche nous garantit plus de contrôle sur le processus de catégorisation et peut produire des résultats plus cohérents et reproductibles.

Choisir l’approche de catégorisation

Cette problématique de catégorisation des exercices de musculation correspond à un cas de clustering non supervisé en machine learning. Nous ne disposons pas de catégories préexistantes et l’objectif est de laisser l’algorithme identifier lui-même des groupes cohérents à partir des caractéristiques du dataset.

Comme présenté précédemment, les modèles de LLM, bien que puissants, présentent des limites importantes pour ce type de tâche. À l’inverse, une approche de machine learning classique offre un cadre rigoureux et transparent pour explorer la structure des données.

Ainsi, le choix du clustering non supervisé s’impose naturellement pour découvrir et analyser les catégories d’exercices de musculation.

Feature extraction : vectorisation des données pour le clustering

Préparation des données pour le clustering IA

Les modèles de machine learning classiques ne peuvent pas traiter directement des données textuelles ou structurées comme le JSON. Il est nécessaire de transformer nos exercices en vecteurs numériques.

Pour ce faire, la première étape consiste à transformer le JSON de chaque exercice en un vecteur contenant les caractéristiques sous forme de variables statistiques :

• valeurs numériques continues,
• valeurs numériques discrètes,
• valeurs ordinales,
• ou valeurs catégorielles.

Stratégie de transformation des caractéristiques en variables

Les caractéristiques de fatigue systémique et de plan de mouvement sont déjà sous forme numérique, mais les listes de muscles et d’articulations sont des listes de chaînes de caractères. Cela signifie que ces listes doivent être converties sous forme numérique.

Multi-Hot Encoding pour la feature extraction

Les modèles de machine learning classiques ne peuvent pas traiter directement des listes. Il est donc nécessaire de choisir une méthode de transformation adaptée.

Dans notre cas, la méthode la plus simple et efficace est le Multi-Hot Encoding. Cette méthode consiste à créer une colonne numérique pour chaque muscle et articulation possible dans le dataset. Cela représente un nombre de colonnes important, mais permet de capturer précisément la présence et le rôle de chaque muscle et articulation dans chaque exercice.

• Les articulations : la représentation la plus adaptée pour les articulations est binaire (1 = impliquée, 0 = non),
• Les muscles : pour les muscles, il est pertinent de capturer le rôle de chaque muscle dans l’exercice. J’ai choisi la représentation suivante :
  • 0 : muscle non impliqué.
  • 0.2 : muscle stabilisateur.
  • 0.5 : muscle secondaire.
  • 1.0 : muscle principal.
  • 1.08 : muscle spécifiquement ciblé.

Création des vecteurs des exercices de musculation

Afin de créer un dataset exploitable pour le clustering, j’ai écrit un script Python qui transforme chaque exercice en un dictionnaire de variables et qui contient le nom de l’exercice pour s’en servir comme index.

La bibliothèque Pandas permet ensuite de convertir cette liste en un DataFrame, où chaque colonne représente une caractéristique. Les valeurs manquantes sont remplacées par des zéros, ce qui produit un dataset complet !

Entraînement du modèle K-Means pour le clustering des exercices de musculation

Choix de l’algorithme K-Means pour le clustering IA

Pour cette tâche de clustering non supervisé, j’ai choisi d’utiliser la librairie scikit-learn, qui offre une large gamme d’algorithmes de clustering.

Après avoir exploré la documentation officielle et analysé mon contexte, j’ai retenu l’algorithme K-Means qui me semble le plus adapté à notre problématique.

Détermination du nombre optimal de clusters avec les méthodes de scoring

L’algorithme K-Means nécessite de définir à l’avance le nombre de clusters (K) que nous souhaitons identifier dans les données.

La détermination du nombre optimal de clusters est l’étape la plus difficile puisque nous voulons éviter de biaiser les résultats en choisissant un K issue de nos propres expériences.
La seule stratégie qu’il nous reste est d’essayer différentes valeurs de K et d’évaluer la qualité des clusters obtenus pour chaque valeur.

Pour déterminer la qualité des clusters, nous allons nous baser sur deux méthodes de scoring couramment utilisées en clustering non supervisé :

• Le score de la silhouette : qui mesure à quel niveau les points d’un même cluster sont proches les uns des autres par rapport aux points des autres clusters. Un score proche de 1 indique des clusters bien séparés, tandis qu’un score proche de -1 indique des clusters mal définis.
• Le score de Calinski-Harabasz : qui évalue la dispersion intra-cluster par rapport à la dispersion inter-cluster. Un score élevé indique des clusters denses et bien séparés.

Coder la recherche du K optimal

Pour automatiser la recherche du K optimal, nous pouvons coder un script Python qui itère K sur la plage de valeurs de 2 à 50 et calcule les deux scores cités précédemment.

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, calinski_harabasz_score
from sklearn.preprocessing import StandardScaler

# Charger les données
df = pd.read_csv('exercises.csv', index_col=0)

# Normaliser les données
scaler = StandardScaler()
nds = pd.DataFrame(scaler.fit_transform(df), columns=df.columns, index=df.index)

# Calcul des scores des différents K
scores = []
for k in range(2, 50):
    print(f"Clustering with k={k}...")
    model = KMeans(n_clusters=k, random_state=0)
    labels = model.fit_predict(nds)

    scores.append((
        k,
        silhouette_score(nds, labels),
        calinski_harabasz_score(nds, labels)
    ))

scores_df = pd.DataFrame(scores, columns=["k", "silhouette", "calinski_harabasz"])
scores_df.set_index("k", inplace=True)

# Analyse graphique des scores
fig, ax1 = plt.subplots()

color1 = "tab:blue"
color2 = "tab:orange"

# Axe 1 : Silhouette Score
ln1 = ax1.plot(
    scores_df.index, scores_df["silhouette"], color=color1, label="Silhouette Score"
)
ax1.set_xlabel("Number of Clusters (k)")
ax1.set_ylabel("Silhouette Score", color=color1)
ax1.tick_params(axis='y', labelcolor=color1)
ax1.set_title("Scores vs Number of Clusters (k)")

# Axe 2 : Calinski-Harabasz Score
ax2 = ax1.twinx()
ln2 = ax2.plot(
    scores_df.index, scores_df["calinski_harabasz"], color=color2, label="Calinski-Harabasz Score"
)
ax2.set_ylabel("Calinski-Harabasz Score", color=color2)
ax2.tick_params(axis='y', labelcolor=color2)

# Combiner les légendes des deux axes
lns = ln1 + ln2
labels = [l.get_label() for l in lns]
ax1.legend(lns, labels, loc="lower right")

plt.show()

Analyse des résultats du clustering IA

En exécutant ce script, nous obtenons un graphique qui montre l’évolution des deux scores en fonction du nombre de clusters K. Cela nous permet d’identifier visuellement les valeurs de K qui maximisent les scores.

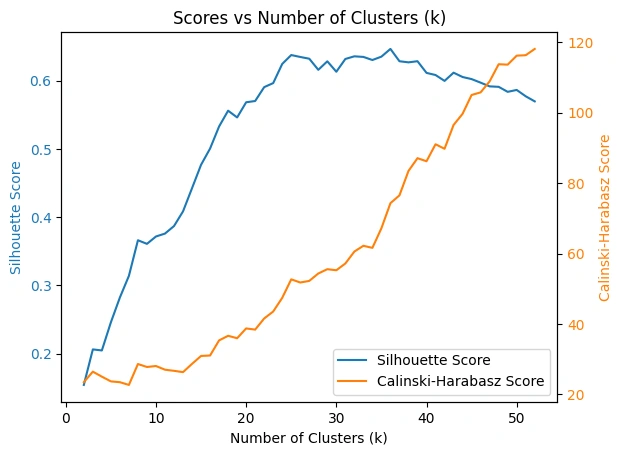
Nous observons que le score de silhouette se stabilise autour de 0.62 pour des valeurs de K entre 24 et 40, tandis que le score de Calinski-Harabasz ne cesse d’augmenter avec l’augmentation de K.

En analysant plus finement les données, nous constatons un pic de score de silhouette à K=25 et K=36. Cependant, le score de Calinski-Harabasz est plus élevé pour K=36 que pour K=25.

A ce stade, nous pouvons en conclure que K=36 est probablement un bon choix pour le nombre de clusters.

Conclusion

Nous avons franchi une étape clé dans la catégorisation des exercices de musculation :

• Choix d’une approche machine learning classique pour garantir la reproductibilité et la transparence.
• Transformation du JSON en vecteurs numériques adaptés au clustering.
• Recherche du nombre optimal de clusters grâce à des métriques objectives (silhouette, Calinski-Harabasz).

La prochaine partie sera consacrée à l’analyse qualitative des clusters obtenus et à la comparaison avec une catégorisation humaine.

Vous avez des questions, des remarques ou des suggestions sur la méthodologie ? Partagez-les en commentaires !